By Haris Aziz
“No invasions of the constitution are so fundamentally dangerous as the tricks played on their own numbers, apportionment, and other circumstances respecting themselves”
–Thomas Jefferson
As the Supreme Court case about the allocation of reserve seats in Pakistan dragged on, the fundamental mathematical principle underpinning the issue was unfortunately partially obscured by courtroom theatrics, red herrings, and election procedure technicalities. I want to discuss the issue purely from a mathematical perspective.
Read more: National Assembly condemns call of US House to probe Feb 8 elections
The Pakistan constitution stipulates that the national and other assemblies have certain seats reserved for women and for non-Muslims. These seats are given to parties through the proportional representation system on the basis of the total number of general seats secured by each political party. The concept of proportionality dates back at least to the ancient Greeks. Euclid defined proportionality in his book Elements (Book VII) as “Numbers are proportional when the first is the same multiple, or the same part, or the same parts, of the second that the third is of the fourth.” Aristotle, emphasised proportionality as a foundational principle for fairness and representation: “equals should be treated equally and unequal unequally”.
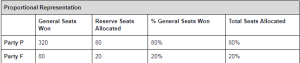
Let us take a simple hypothetical example to explain the maths behind this issue. Suppose there are 500 seats in the Republic. Among these 500 seats, 400 are general seats that are contested via elections whereas the remaining 100 are reserved seats that are allocated to the parties in proportion to their wins. Suppose there are two hypothetical parties: Party P and Party F (Favoured). Suppose P won 320 out of the 400 general seats and F won 80 out of the general 400 seats. Since P won 80% of the general seats, proportional representation requires that it gets 80 of the 100 reserved seats as well. Similarly, since F won 20% of the general seats, in a logical and mathematically consistent world, it would get 20 of the 100 reserved seats as well.
Now if someone really wanted to pretend that P is not a valid party, it may lead to problematic legal issues that lawyers and political scientists are best suited to comment on. In this case, I mainly want to highlight a basic mathematical contradiction. There are two natural options if we close our eyes and pretend that P does not exist as far as reserved seats are concerned. Let us examine the options one by one. One option is called Vanish, and the other is Gift.’
Read more: India elections 2024: What challenges await new government?
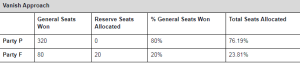
The Vanish approach is that the 80 reserve seats claimed by P are made to vanish into thin air! In other words, these seats are left unused. This is already problematic as there is a basic mathematical requirement that there be a total of 500 seats, including 100 reserved seats, that are to be filled up and then used for assembly decisions. Let us ignore that requirement for now and do the numbers.
The updated total number of seats would be 400+20 = 420. In that case, F could get its deserved 20 seats, and the other seats are simply unfilled. But let’s see what happens in that case. F now has (80+20) out of the total 420 seats which is more than 23.8% of the used seats. And what happens to P? It gets 320 / 420 seats, which is 76.19%, which is less than the deserved 80%. Under the Vanish approach, not only is the assembly incomplete but the parties get the wrong proportion of seats.
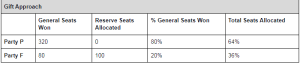
Let us now consider the Gift approach, which respects the requirement that all 100 reserved seats must be used. If there is an insistence that P must not get its 80 reserve seats, then the option (as ludicrous as it may sound) is to give them to the favoured party F. This ensures that all reserved seats are used. However, it leads to the following. F gets a total of 100+80 seats, which is 36% (180/500) of the total used seats. Considering that the F only deserved 20% of the seats, the approach contradicts proportionality. On the other hand, P, which deserved 80% of the total used seats, now gets 64% (320/500). Under the Gift approach, the level of injustice is extreme as the favoured party F gets seats it has no claim on.
One thing that needs to be mentioned is that when parties are given seats in proportion to their strengths, the allocation may not be absolutely perfect. For example if some party wins 80.5% of the seats, it can claim 80.5 of the 100 reserved seats. But since seats cannot be given partially, it will either get 80 or 81 seats (variation is at most one). There is a vast literature in mathematics and political science on what is the best way to round the numbers which is referred to as apportionment.
There are several apportionment methods that have been invented, each with its own merits. Many of the theoretical developments around rounding methods arose from principles that grew out of political contests in the course of United States history. Several of the methods are named after American presidents such as John Adams and Thomas Jefferson. Daniel Webster (Former US Secretary of State) stated that “to apportion is to distribute by right measure, to set off in just parts, to assign in due and proper proportion”. What is clear is that if a party that is expecting 80.5 reserved seats gets less than 80 seats, it will feel that a grave injustice has been done.
Mathematics provides the foundation for a reasoning society. What we have illustrated by a simple example is that methods such as Vanish or Gift that deprive a party of its share end up contradicting the mathematical principle of proportional representation. An extreme approach which maintains proportional representation of the parties is to completely do away with reserve seats. However, not only does that mess with the total number of seats but it also deprives minorities and women of crucial avenues for representation.
Many issues around proportionally allocating reserved seats are discussed in legal jargon or with the lens of realpolitik or election procedures. However, as far as the constitution and fundamental mathematics are concerned, there is only one consistent solution. That solution is to respect proportionality as required by the constitution, allocate all the reserve seats, and do so in proportion to the seats won by the parties.
Haris Aziz is an academic at UNSW Sydney. He can be reached at haris.aziz@unsw.edu.au. His x.com account is @harisazizk
The views expressed by the writers do not necessarily represent Global Village Space’s editorial policy.














